2015-April-13 Lab 13: Magnetic Potential Energy

Magnetic Conservation of Energy

Jenna Tanimoto

Lab Partners:  Jacqueline Dagdigian, Changmin Han

April 13, 2015

PURPOSE:  To find an equation for magnetic potential energy and verify that conservation of energy applies to a system with magnetic potential energy and kinetic energy of a cart.

PROCEDURE:

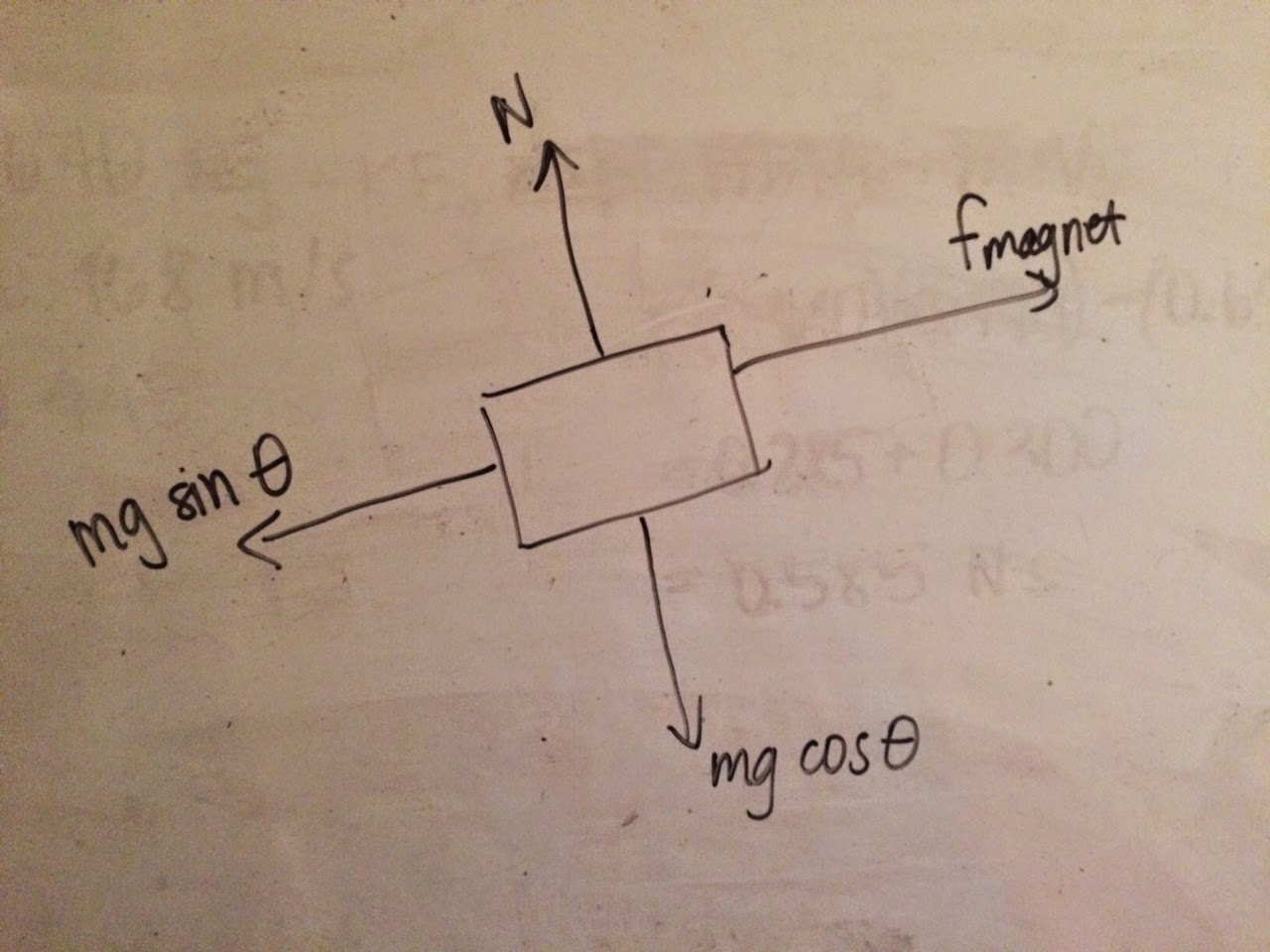
Set up to find potential energy at 5 angles.

In order to find an equation for magnetic potential energy, we set up a system where magnetic potential energy between two magnets was equal to gravitational potential energy.  We did this by placing a cart on an air track with a magnet at the end of the track facing towards the magnet on the cart, and raising one end of the air track to an angle.  We let the cart slide down to a point of equilibrium (where it was still and some distance away from the magnet), letting this magnetic potential energy equal gravitational potential energy.  We then measured the angle of the air track and  the distance between the two magnets to find force as a function of their separation distance.  We repeated this at 4 more angles and collected the following data:

We used this force diagram to show that the magnetic potential energy is equal to mass times gravity times sine of the angle of the air track.

We plotted force and separation distance to achieve the following graph and fit a power curve of F=Ar^n to the points.  This gave us an equation of y=7.975e-5 * r^-1.937:

Force (y-axis: N) vs. Separation Distance (x-axis: meters)

Using the relationship between force and separation distance, we integrated the function to find a function U(r) between the magnets:

Function for magnetic potential energy.

To verify that conservation of energy applies to this system, we ran one more experiment.  This time the air track was laid flat, and we ran a motion detector as the cart was pushed towards the other magnet, the system collided, and the cart returned towards the starting position.  This experiment collected the position of the cart, velocity, and separation distance.  From this we were able to calculate kinetic energy (KE = 1/2mv^2), magnetic potential energy (Umag = 8.511e-5*r^-0.937), and the total of both KE and Umag giving us the following graph:

 This graph shows that when we add up the kinetic energy and magnetic potential energy, the total energy stayed about the same, even during the collision.  This means that energy was conserved

CONCLUSION:

In our lab we were able to derive an equation for the force between two magnets, and prove that this force was conserved during an experiment with potential magnetic energy and kinetic energy.  In our graph for total energy, the energy fluctuates at a few points.  This could have been because there was an uneven part of the air track which caused kinetic energy to change.  There also could have been fluctuations in air resistance as the cart was moving.  Another error could have resulted from being off on our measure of separation distance.  Because the distance change was less than a centimeter each time, being off by a little made the point on the graph far off from the resulting curve.