PURPOSE: To verify that the impulse-momentum theorem holds true during three different collisions.
MATERIALS:
We ran the experiment, and the cart comes to rest after the collision. We obtained the following data:
CONCLUSION:
In all three experiments (1) elastic collision with some mass, (2) elastic collision with greater mass, and (3) inelastic collision with greater mass, the impulse and change in momentum were nearly equal to each other. Impulse and change in momentum are greater when using a larger mass. Both are also about half the value during an inelastic collision, because the time span for an inelastic collision is smaller.
Our results were about 7-8% in error, which could have been caused by nicks or uneven parts of the track, altering the initial and final velocities. The spring that we used may not have been of the highest quality.
MATERIALS:
- Cart with a spring plunger contraption (plastic spring bit can be pushed in and springs out)
- Second cart that moves on a track
PROCEDURE:
Experiment 1:
- Set up track with a moving cart on one end, with force sensor placed on top
- Replace the hook of the force sensor with a rubber stopper
- Clamp stationary cart (with spring plunger attached) to a rod clamped to the table on the other end of the track (see below)
- Set up so that spring plunger and rubber stopper hit one another during a collision
- The motion sensor should be placed on the end of the track opposite the stationary cart
- To begin the experiment, we opened a pre-setup LoggerPro file called Impulse and Momentum, and made sure to calibrate and zero the force sensor
- To run the experiment, we simply pushed the cart towards the spring plunger and let it bounce back
- The data we got from this experiment was graphed on two graphs:
- Velocity (m/s) vs. Time (s)
- Force (N) vs. Time (s)
The first graph from above shows velocity of the cart before it hits the spring plunger, while it is hitting, and after it bounces back. Using this data, we can find the change in momentum of the cart. Before the experiment, we measured the mass of our cart to be 0.640 kg. We used the examine tool to find the velocity of the cart before collision and after collision and plugged it into an equation for change in momentum:
The amount of momentum change resulted in 0.585 N s. According to the impulse-momentum theorem, the change in momentum for the moving cart is equal to the total impulse acting on the cart. The total impulse can be found by taking the area under the force and time graph during the collision. In our situation we used the integration tool to integrate Force x time during the collision, and found the area to be 0.5442 N s. These results show that our change in momentum and net impulse are within 7% of each other.
Part of why this is off could be because the before and after velocities of the cart varied. This could be due to an imperfect spring bumper that causes an elastic collision that is not perfect. It could also be due to variations in the track.
Experiment 2:
For the next part we added 200 grams to the cart and then ran the same experiment to collect the following data:
Again, we found the total impulse by integrating the force x time graph during the collision. This value was 0.6998 N s. We also calculated the change in momentum using initial velocity, final velocity, and mass:
Change in momentum resulted in 0.759 N s. Impulse and change in momentum were within 8% of one another. Using a more massive cart made impulse and change in momentum less equal to each other by a small amount. However, this should not have been the case. They should have been consistently equal to each other in both experiments because the mass of the cart stays the same during the collision. The results may have been off again in this experiment due to the same factors that were caused in the previous.
Experiment 3:
For the last trial, we replaced the stationary cart with a block of wood that had clay attached to it, and replaced the rubber stopper with a nail. This causes an inelastic collision on impact.
Again, we found the integral for the period of collision, which was 0.3869 N s. Calculating change in momentum, we have:
 |
| Change in momentum, with final velocity as 0. |
In this situation, the results again are within 7% of each other. We predicted that even in the inelastic collision, impulse and change in momentum would equal each other.
We can also notice that impulse in this inelastic collision is about half the impulse of the elastic collision with the same mass. We had predicted that the impulse would be less for the inelastic collision because it is over a shorter period of time.
CONCLUSION:
In all three experiments (1) elastic collision with some mass, (2) elastic collision with greater mass, and (3) inelastic collision with greater mass, the impulse and change in momentum were nearly equal to each other. Impulse and change in momentum are greater when using a larger mass. Both are also about half the value during an inelastic collision, because the time span for an inelastic collision is smaller.
Our results were about 7-8% in error, which could have been caused by nicks or uneven parts of the track, altering the initial and final velocities. The spring that we used may not have been of the highest quality.




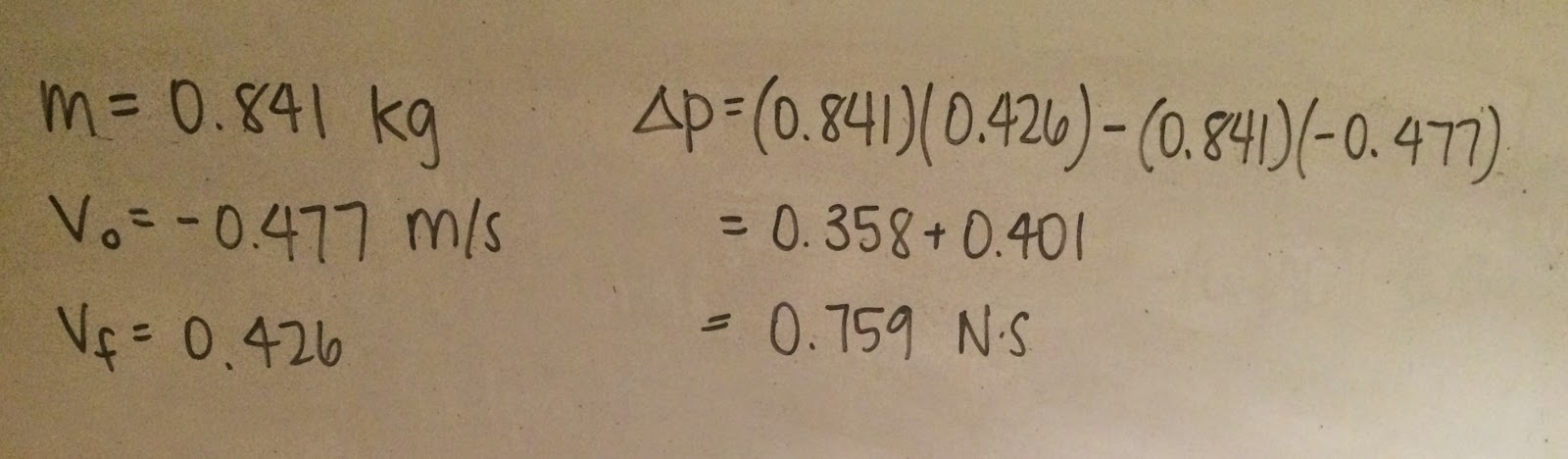




.png)

.png)

























